現代のコンピューターの発明に続く「情報」という基礎的な概念をつくったのがクロード・エルウッド・シャノン（Claude Elwood Shannon；1916-2001）という人物だ。本記事では、シャノンの提唱した情報理論を数式を使わずに解説し、「情報とはなにか」を掘り下げる切り口を紹介する。
「価値ある情報を高速に、正確に送りたい」
シャノンは、「情報」という概念をつくった人物で、「情報理論の父」とも呼ばれる。ここでいう情報をつくったというのは、言い換えると「さまざまな情報を数値に置き換えて表すことができる」ことだ。
情報を数値化することでシャノンが行ったのが、「情報通信」の基礎理論の構築であった。シャノンが目指したのは、「価値ある情報を高速に、正確に送りたい」だったと言われる1。
このテーゼからふたつのポイントが抽出できる。ひとつは情報が持つ価値を測る尺度としての情報量や情報エントロピー、もうひとつは情報を高速に、正確に送るための通信の理論についてである。今回の記事では、ひとつ目に絞って紹介する。
情報の最小単位「ビット」──情報量を数値で表す基礎
まず、紹介するのが情報を数値化する方法だ。情報を数値化するというと難しく聞こえるかもしれないが、原理はいたって簡単。昼飯でなにを食べるかという例で、ご飯ものを食べたい気がするが、麺類もありかもという状況で、これらの選択肢≒情報を数値化してみよう。ご飯ものと麺類の2択で、「はい」を1、「いいえ」を0とすれば、下記のようになる。
| 1：ご飯もの | 0：麺類 |
でも、普通はもっと食べたい種類がたくさん出てくるはずだ。ここで選択肢を4つにし、迷いどころであった「ご飯もの」かいなかを「1：はい」「0：いいえ」で選ぶこととする。
| 1：ご飯ものにする？ はい | 0：ご飯ものにする？ いいえ |
| ごはん定食 | ラーメン |
| からあげ定食 | うどん |
この「はい」「いいえ」に答えると、選択肢はそれぞれ2つに減ることになる。仮にやっぱり麺類を選んだとたら、中華系や和食系の2択でさらに選択肢を1つに絞ることができる。ということは、2回の質問で4つの情報が表せる。
選択肢が8つの場合でも、1回目の質問で選択肢は4、2回目の質問で2、3回目の質問で答えが確定する。つまり、1回ごとに「はい」「いいえ」で答えられる2択の質問をすると選択肢は半分になる。なので、1024個の質問があった場合は、
1024→512→256→128→64→32→16→8→4→2→1
10回の質問で答えを1つに絞れる。逆に言えば、10回の質問で1024通りの情報を表すことができる。この2択で表せる情報の最小単位が「ビット（binary digit）」と呼ばれ、こうして曖昧な情報をシャノンは数値で表した。
シャノンの通信モデル──情報伝達回路を数値化したもの
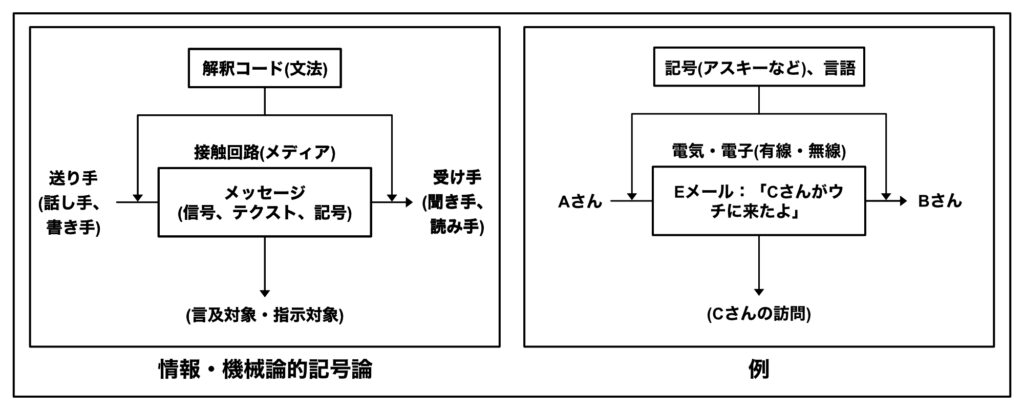
シャノンの通信モデル（こちらの記事で情報伝達モデルと言及したものと同じもの）は、情報（メッセージ）を送り手が受け手に向けて伝達する過程にある要素が6つある。ここでイメージしてもらいたいのが、基本的に情報は接触回路を介することでノイズが入り込み、受け手に届いたとしても情報の復元（解釈）が行われ、正確なメッセージそのものの伝達が困難だという点だ。
特にシャノンが活躍する20世紀前半には、正確な情報伝達が困難だったことは想像に難くないと思う。あくまで情報通信のモデルで、正確で早いメッセージ伝達を目指したシャノンの背景はここにある。だからこそ、通信モデルでは6つの要素が数学的に定義され、通信上の情報量を減らし、ノイズ≒誤りの制御が試みられた。
この点を詳細に説明すると、細かくなってしまうので割愛するが、通信量を減らす理論が「情報源符号化定理（シャノンの第一基本原理）」、誤りを減らすのが「通信路符号化定理（シャノンの第二基本原理）」と呼ばれている。
情報エントロピー──情報の「面白さ」を表す価値尺度
まず、情報の価値とは、情報がない状態に比べて、情報を手に入れることで得られる価値のことである2。情報の価値を感じる好例が天気予報だ。オフィスから帰る予定の1時間後に「雨が降る」ことがわかるのは、その情報を知らない状態に比べて明らかに高い価値がある。この情報の価値を数式化したのもシャノンであった。
情報エントロピー
情報エントロピーとは、情報量の期待値である。ここでいう期待値とは、期待が寄せられるものの大小のことで、期待が高ければ情報エントロピーは高くなる。俗っぽい表現をすると、情報エントロピーが大きいということは、それだけその情報が「面白い」ことを表している。
情報エントロピーを数式化する上で使われるのが、「情報の大きさ」と「情報が出現する確率」だ。以下、順に紹介する。
情報量
シャノンが行った特異なことのひとつが、確率という観点から情報量を定義したことだった。情報量は、それが起こる確率とその価値の関係から定義される。起こる確率が低いものほど、その情報の価値が高い。逆に、起こる確率が高いものほど、その情報の価値は低い。
だから、絶対に起こる出来事の情報量は0になるし、（計算は省くが）等確率で100回に1回しか起こらない出来事の情報量は7ビットになる。基本的に二者択一で選ぶため、情報量はある出来事が起こる「手間・手数の大きさ」だと捉えることもできる。
情報が出現する確率と価値の関係
いよいよ情報の価値を出来事が起こる確率との関係から考えてみたい。たとえば、竜巻が起こるか、起こらないかの情報量の期待値を考えると、どちらも100%で起こる・起こらないがわかっていればその情報は等しく価値がない。なぜなら、竜巻の発生の是非がわかりきっているなら、その起こるか起こらないかの確率に対する情報への期待はまったくない。
つまり、わかりきっていることの情報エントロピーは、出来事が起ころうと起こらないであろうと0だ。では、起こるか起こらないかの確率が2分の1だったとしたらどうだろう。この場合、竜巻が起こるかどうかの情報をなんとしてでも得たいはずで、この際にこの情報の価値は最大化する。
竜巻の例でわかるように、情報エントロピーが大きい状態とは、「結果の予測ができない状態」「情報が曖昧な状況」であり、そのためこれから得る情報の価値が大きいことを表している。
シャノンの情報通信理論では、この情報エントロピーは、情報が通信路を通る速度として扱われている。ゆえに、高速で情報を送るためには、情報エントロピーを最適化することが目指される。
おわりに──情報とはなにか
以上、高岡詠子さんの『シャノンの情報理論入門』（2012年、講談社ブルーバックス）を参考にシャノンの情報理論の一部を解説した。本記事は、情報を数式化したシャノンの理論の中身をざっくり紹介することを目的したものとなっている。というのも、情報科学としてではなく、人文学の観点から「情報とはなにか」を考える糸口にできればと思ったからだ。最後にその背景について少し紹介したい。
現代はよく情報社会と言われるように、インターネット上には日夜、情報が渦巻き、スマホの存在は社会と分かち難く結びついている。どこにでもあり、記録できるのが「情報」だが、その実態を見えるかというとそう簡単にできない。情報とはなにかを考えることは案外難しい。
情報機械技術がコンピューター、インターネット、スマートフォンをはじめとした環境として当たり前となったいま、「情報とはなにか」を考えることはしにくいはずだ。というのも、情報技術の席巻により、情報発信の担い手を増やし、情報社会で人々が市民として活躍する未来が夢見られてきた。だが、これらはいずれもその人々が情報社会で「経験」するものであって、「情報」そのものへの着目にはつながったものとは言い難い。
グローバル化し、消費社会となり、情報技術によって確かに人々の選択肢は増え、経験できることは増えた。けど、環境そのものへの着目もさることながら、もっとずっと深層に「情報とはなにか」という問いがある。シャノンの情報理論は、現実からデジタルへと変換し、情報の価値・面白さを確率から考えるという、情報を考える初期の入口を提示してくれている。
参考文献
高岡詠子（2012）『シャノンの情報理論入門 価値ある情報を高速に、正確に送る』（講談社ブルーバックス）